
Mirko Baum: Form follows science
My task was not to preach God, but to serve God and to remain silent about God.
In 1934, a photograph of a skinny man, assisted by a reporter from NBC, emerged in the global press as he squeezed his long legs through a narrow 35-centimeter opening into the interior of a small iron sphere. This man was American zoologist William Beebe (1877-1962) and the cast-iron sphere, equipped with three small windows made of thick silica glass aside from the entry hole, was an instrument for exploring ocean depths. Beebe's friend, geologist and sphere designer Otis Barton, named his invention the "bathyscaphe." Within this 32-millimeter thick sphere, which had a diameter of just under 150 centimeters, both scientists undertook a series of descents, the most famous of which was the dizzying descent conducted in August 1934 in the Bermuda area, (1) which led to a depth of 923 meters previously unattained by anyone. This experiment coincided almost simultaneously with the ascent of Swiss researcher Professor Auguste Piccard (1884-1962) into the stratosphere. The aluminum gondola carried by a balloon with a maximum volume of 14,000 cubic meters was remarkably similar in shape and size to the bathyscaphe; however, due to the opposite direction of pressure effects, it required only a tenth of its thickness, amounting to just 3.5 millimeters in this case.
Unlike Beebe's "Russian roulette" descent, the danger of Piccard's ascent to a height of sixteen thousand meters was quite calculable, which in no way applied to the dangers associated with the inevitable return to earth. Auguste Piccard and his assistant Paul Kipfer likely did not devote too much attention to the landing issue - unlike Piccard's mother! She arrived at the site moments before takeoff and brought two wicker baskets, lined with soft cushions of her own making, to protect the precious heads of both researchers from undesirable damage. Just like Beebe's preparations before the Bermuda descent, the photograph of both serious scientists with quirky hats on their learned heads went down in the history of research as well as into the annals of subtle Swiss humor.
More than through his ascent into the stratosphere, "vertical professor" Piccard became famous for his oceanographic research, specifically the exploration of ocean depths using a submersible named "bathyscaphe." Just like the gondola of the airship, suspended from a body filled with hydrogen or helium, the gondola of the bathyscaphe is suspended from a float filled with gasoline. Just like an airship, the bathyscaphe also changes its position horizontally through motor power and vertically by taking in or releasing weight. The gondola of the bathyscaphe is also spherical, this time with a wall thickness of 90 mm. Unlike the bathyscaphe, molded from one piece, the gondola of the bathyscaphe is forged from two steel hemispheres. Since technically it is almost impossible to dimension the connection of both hemispheres to the pressures that vary with the depth reached (for example, by connecting with screws), the two hemispheres are glued together with Araldite after careful processing of the contact surfaces, the role of which, just like that of a relatively thin steel band in the connection area, is to prevent their mutual displacement. The perfect sealing of this ingeniously simple construction occurs automatically, in intensity corresponding to the depth reached.
This intelligent detail reminds us of a famous experiment carried out in 1663 by the learned mayor of Magdeburg Otto von Guericke (1602-1686), when he demonstrated that two freely placed spheres could withstand the force of a strong horse team when air was pumped out. This experiment was also associated with considerable personal risk. Matter was considered to be the expression of the Creator's will, as it was the only proof of His creative existence. From this perspective, a vacuum could therefore not exist, and the assertion of the opposite, i.e., the assertion of the existence of "nothing," was in the days when Aristotle's teaching on "horror vacui" was still an unshakable dogma of scholastic science, a life-threatening blasphemy.
From the described experiments, it is evident that a sphere is an ideal boundary between two different environments, whether as a protective shell of an "artificial living environment" or as a cover for "nothing." Scholastics, alongside Aristotle, believed in the finitude of the cosmos and its delimitation by a spherical surface as a perfect God-given form. The "heavenly dome" had already become an architectural metaphor for the builders of antiquity, and its architectural representation was both a cultural necessity and a significant technical problem calling for resolution.
The dome of the Roman Pantheon, with a diameter of 43.2 m, is, when viewed from the inside, an exact hemisphere. It rests on a cylindrical drum, the height of which is equal to its radius, so it is possible to inscribe a sphere into the enclosed space, whose upper hemisphere completely fills the dome, while the imaginary lower hemisphere touches the floor at its exact geometric center with its "south pole." The fact that this magnificent structure has stood for nearly two millennia may be considered the most convincing evidence of its static capability; however, debates regarding the physical nature of this capability are still ongoing.
Today we know that the course of loading in a dome constructed of material capable of carrying only pressure acts along a curve corresponding to the shape of an inverted catenary. This curve must be demonstrated in approximately the inner third of the statically effective cross-section to prevent the proposed construction from collapsing. From shell theory, we know that the upper part of the spherical dome is stressed by a centripetal horizontal component of forces, while its lower part is stressed by a horizontal centrifugal component. The reversal of both forces occurs at the intersection point of the upper hemisphere with a cone whose apex is located at the south pole of the lower hemisphere, and whose apex angle is approximately 51°. In a dome constructed of material capable of carrying only pressure, inevitable tearing of the structure occurs at the intersection point. To avoid this catastrophe for the Pantheon, it was necessary to adopt measures, of which this building offers several:
First, the sectional view reveals that the thickness of the masonry in the dome increases from top to bottom, from the opening (oculus) with a diameter of nine meters, which is somewhat its "lightest" part, down to the stepped external accumulation of mass in its lower part, whose role is to enhance the vertical component of forces through increased mass, thus bringing the resultant vector closer to the imagined catenary.
Second, the construction of the Pantheon is divided into several sectors, differing in the weight of the employed masonry. From bottom to top, the travertine of the foundational masonry alternates with a mixture of travertine and limestone in the lower section of the drum. The upper part of the drum and the lower part of the dome up to the level of the second ring of coffers are built of limestone; a mixture of limestone and brick serves as material at the third ring of coffers, and finally, a mixture of limestone and pumice is the masonry of the remaining upper portion of the dome.
Third, the interior side of the dome features twenty-eight coffers in five overlapping circles, whose dimensions—namely, width, height, and depth—increase downward due to the growing circle. In other words, while the ribs of the coffers limit the spherical surface, their bottoms limit the statically effective area, which, with the varying depth of the coffers, approaches that of a rotational paraboloid, i.e., the ideal shape of a pressure-loaded dome.
Proving this hypothesis was the objective of a research project undertaken by Reiner Graefe and Frei Otto at the Institute for Lightweight Structural Engineering at the University of Stuttgart. (2) The work began with a two-dimensional chain model, on which the catenary was represented as the resultant of the known weight of the masonry and the proposed annular forces. The unknown component of horizontal annular forces was simulated by chains of constant length (and hence constant weight), suspended above the point of their effect, so that the curvature could be inferred for the sought horizontal component. The acquired data were then entered into the final three-dimensional model to depict the course of forces in their overall influence. Here, the annular forces were represented by chain parallelograms, whose deformation corresponded to the magnitude of the horizontal force vectors in the corresponding section of the arch.
This experiment was, of course, merely a demonstration of a presumed situation and does not exclude further hypotheses. One of the other possibilities is elaborated by Dirk Thode in his dissertation (3) - he considers the upper part of the dome, i.e., the part that is centripetally stressed up to the point of force reversal, as a spherical shell and only proves the catenary below this plane. Perhaps the second hypothesis is somewhat closer to the truth; in any case, it receives intriguing support from the geometric analysis of the structure (4) performed by Otto Schubert. The triangulation of the Pantheon does not rest, as for example in the Hagia Sophia in Constantinople, on an equilateral triangle with an angle of 60° (5), but on an isosceles triangle with an apex angle of 51° 51' 14", i.e., with considerable accuracy concerning an angle known only to engineers of our time, and that from the aforementioned theory of shells. This affinity of form and its static arrangement is fascinating. It is a testament to the high technical level of a building that fully exhausts the scientific-technical possibilities of its time. Finally, only the exciting question remains of how much of what we now call shell theory was known to the builders of late antiquity in the early 2nd century AD.
After the construction of the Pantheon and the Hagia Sophia, attempts to realize a spherical dome nearly fell silent for an entire millennium. It was only in the 15th century that they revived with the constructions of the dome of the Florentine cathedral (42 m) and the dome of St. Peter's in the Vatican (40 m). However, these constructions deviate from our theme since they are double-skinned ribbed structures entirely consistent with the geometry of the catenary. In the case of the Florentine dome, spherical geometry was completely abandoned, and in the case of St. Peter's Basilica, its rendering in the soffit is merely an illusion. The scientific and technical significance of the dome of the Vatican temple lies primarily in the theoretical foundations of the statics of vaults, which were documented by savants of the 18th century in their research analyzing the structure and studying the damages that arose.
Entirely beyond the technical possibilities of spherical constructions constructed from material capable of transmitting only pressure (and thus only in projects) remained the spherical archetype of French revolutionary architecture at the end of the 18th century, of which the most famous and technically demanding example is "Newton's Cenotaph," authored by Etienne-Louis Boullée (1728-1799). Unfortunately, even a fleeting look at the construction of the gigantic sphere reveals its unfeasibility. (7) In section, we can recognize the eccentricity of the outer and inner boundaries of the sphere, favorably expressed in the varying thickness of the shell; however, this alone would not prevent the tearing of the structure at the point of reversal of the centripetal and centrifugal horizontal forces, already described in relation to the vault of the Pantheon. From a technical perspective, this gigantic building can at most be considered a visionary foretaste of reinforced concrete structures, which had yet to wait another 70 years. Although Françoise Ciognet (1814-1888) patented concrete as early as 1856, it took another 40 years for this unconventional material to be recognized by the famous École des Beaux-Arts, which only "stooped" to give lectures on concrete structures in 1897.
Boullée's project was both an architectural monument and a scientific instrument. Like the Pantheon, "Newton's Cenotaph" was an architectural representation of a heavenly dome, whose conical openings, symbolizing the starry sky, were directed toward the symbolic sarcophagus of the then greatest scientific authority, the famous English physicist Sir Isaac Newton. Boullée's project was created in 1784, five years before the outbreak of the French Revolution and—more importantly—a year after the ascent of the first balloon by the Montgolfier brothers. The gigantic dimensions and pathos of the work were expressions of a new era, whose horizon was exponentially widened due to the invention of aerostatic flight in both a transferred and a literal sense. The boundless space, i.e., a dimension that was previously only physical, became an imaginary aesthetic dimension. "The idea of greatness dominates our senses to such an extent that even the feeling of horror becomes a part of our admiration." (8) From these words, which Boullée used to comment on his project, resonates the notion of "beauty that terrifies" (horriblement belle), a concept promoted by the English thinker Edmund Burke (delightful horror) and German philosopher Immanuel Kant (die Schönheit des Schrecklichen), which became an integral part of European thinking by the end of the 18th century. In the aesthetic terminology of his time, this notion simultaneously describes "sublimity" (le sublime), which occupies one of the central roles in the architecture of the French Revolution. The temporal and thematic correlation of this new aesthetic dimension with the (relatively useless) invention of the Montgolfier brothers, as well as with the fascination of conquering the aerial sea in general, is evident.
The true expansion of this new aesthetic occurred in 1909 after Louis Blériot's sensational flight across the English Channel. Its most striking literary document is the aggressive staccato of the futurist manifesto published that same year by the Parisian newspaper "Le Figaro." This spirited and shockingly loud "foundation stone" of European modernism, authored by Italian poet Filippo Tommaso Marinetti, not only marked the beginning of a youthful, vital anti-bourgeois movement but was unfortunately also an artistic prelude to the industrial slaughter of both world wars, which plunged the European continent into a brutalism previously unknown and into the loss of cultural identity whose consequences we still feel.
Every reader of gruesome tales knows that horror can only be savored from the position of one's own safety, i.e., from the certainty that the domination of senses will not be followed by the domination of the physical body. In the case of more serious cultural subjects, such as fine arts and architecture, it is currently quite difficult for us to admit this aesthetic dimension, as its association with totalitarian ideologies is more than painful—whose repertoire extends beyond mere aesthetic horror to its physically perceptible realization. Perhaps it is precisely here that we must seek the reason why architecture of the "heroic style" (from Boullée to Speer) is generally rejected by even the most competent architectural critiques (from Sedelmayr to Posener). Nevertheless, this does not change the existence of forms of beauty that continue to tempt our "Faustian soul," regardless of whether we consider this feeling politically correct or not.
The morphological connection of the spherical archetype of the French Revolution with the invention of the aerostat is evident in terms of both a mere formal affinity with this new means of scientific and technological progress and in terms of the ideas of the Enlightenment about the global expansion of revolutionary ideas, the growth of sciences, and social reforms, concerning the political and scientific reconstruction of the world. In this form and with a similar significance, the spherical archetype also survives in the architecture of the Russian proletarian revolution, surprisingly at a time when aerostatic flight had long ceased to be a technically interesting alternative. In 1927, Ivan Ilyich Leonidov (1902-1959) used in his famous project "Institute V. I. Lenin" an aerostat quotation, in a form that in its monumental gesture matched the projects of the French Revolution. This project, which was a graduation work by a twenty-five-year-old student of the Moscow VCHUTEMAS school of art, captivated his contemporaries to such an extent that they prompted the young author to stay another two years at the school as an associate professor. Leonidov's project, which shines today with unparalleled modernity, is often cited as the pinnacle of Soviet constructivism. However, that does not change the fact that the answer to the pressing question of the technical execution of the glazed spherical auditorium, which, similar to "Newton's Cenotaph," was supposed to serve alternatively as a planetarium, remained (as is often the case with student works) a mystery to the author.
The so-called "geodesic construction," still regarded as the optimal technical mastery of spherical forms, is a term loosely related to aerostatic flight. The term was first used by Barnes N. Wallis (1887-1979), who, while working as a designer for Vickers, experimented with "geodesic" nets whose function was to stabilize and protect against damage the gas chambers inside the lifting bodies of English airships. Barnes N. Wallis, who remained true to the "geodesic" theme throughout his fruitful life (9), gained fame in 1933 for the unconventional design of the Vickers "Wellington" bomber, whose "geodesic" structure we would more accurately describe today as a laminate construction. Another expert in the field of aerostatic flight was Austrian aerodynamicist Paul Jaray (1889-1974), (9.1) who passionately debunked the still widely held naive assumption regarding a raindrop taking an aerodynamically clean "droplet" shape during its fall concerning the research of bodies of the least resistance. "Incomprehensible, if not downright miraculous, is the notion of a drop that tapers at the back and its uncritical circulation in literature. Nature has contributed nothing to this alleged 'insight.' (...) Many even believe they have seen the shape of a forward-expanding and backward-pointed drop with their own eyes; this can be explained by the fact that a drop hanging on a solid object adopts an elongated pear shape at the moment it attempts to leave this object due to gravity. This shape is derived from the interplay of gravity and surface tension. As soon as the drop detaches from this object, it takes on a spherical shape, which it then never abandons." (10)
The complementary effects of tension on the surface of a sphere and pressure within it are the cause of the stability of a series of natural forms, of which a classic and frequently cited example in literature is the stable system of cells on the spherical surface of an insect's eye. Karel Honzík, one of the architects of the Czech avant-garde and author of theoretical treatises, writes in his "Reflections on Biotechnics" about the balance between forces "centripetally collective" and "centrifugally individual." (11) This "state-forming" interpretation of a stable system as the result of complementary forces, expressed in the typically leftist jargon of the 1930s, is identical to the "energy-synergetic" theory developed by the multifaceted American engineer and philosopher Richard Buckminster Fuller (1895-1983). The "geodesic dome," for which Fuller is generally considered the inventor, is still recognized as both elegant and the ultimate mastery of the spherical form.
In the "energetic" part of his theory, Fuller separates local functions, while the "synergetic" part refers to natural organizing schemes that derive their stability from the synergetic interaction of complementary functions. In the case of the geodesic dome, it is the complementary properties of two Platonic bodies, the tetrahedron (a polyhedron with four equilateral triangles) as the fundamental scheme for the organization of matter in general and the icosahedron (a polyhedron with twenty equilateral triangles), which has properties that most closely resemble a sphere. Of all the regular polyhedra, the tetrahedron encloses the smallest volume with the greatest surface area, while the icosahedron, like a sphere, encloses the greatest volume with the least surface area. The tetrahedron and the icosahedron behave complementarily even under physical load. While the tetrahedron represents a form advantageous for loading with pressure, the icosahedron, like the sphere, represents a form advantageous for loading with tension. The connection of these complementary bodies occurs by joining the centroid (center) of the icosahedron with its twelve vertices, thus creating a concentric spatial truss of twenty tetrahedrons linked into a single icosahedron.
This seductive hypothesis, however, is unfortunately only an apparent possibility. The sides of the triangles on the surface of the icosahedron are actually about 5% longer than the sides directed towards its center. (12) This fact, which is referred to by solid-state physics as "frustration," leads to the conclusion that the compact assembly of spheres does not grow into an increasingly larger icosahedron, but forms what is known as a cuboctahedron, i.e., a polyhedron whose surface consists of eight equilateral triangles and six squares. By missing triangular connections at six points on this imagined spatial truss, this form is unstable. For this reason, the organizational scheme of matter based on the five-fold symmetry of the icosahedron was long excluded. This "attack" on "energy-synergetic" theory, however, did not stand in the way of the ingenious construction that Fuller patented in 1954 and successfully used in numerous military and civil constructions, including the USA Pavilion at Expo 67 in Montreal, Canada. (13)
The problem of "frustration," however, is not the only shadow cast over the work of the American genius. In the early 1920s, the German Museum in Munich requested a project and the execution of a star projector from the Zeiss company in Jena, which was to become a part of the Munich planetarium. Walther Bauersfeld (1897-1959), who was commissioned with this work, developed not only the optical appliance but also the spherical shell construction, which was to serve as a projection surface. The resolution to this problem was described by Bauersfeld in his notes as follows: "If we imagine a regular body, the surface of which consists of twenty equilateral triangles, and we trim each of its twelve corners with a flat cut, we obtain a surface consisting of twenty hexagons and twelve pentagons. It is easy to choose the plane of the cut in such a way as to circumscribe both polygons with a circle of the same radius. The projection from the center of the resulting structure onto the surface of a sphere with the same center will then create an even distribution of the sphere." (14) Bauersfeld's prosaically and without "energy-synergetic" described process is nothing but a depiction of the geodesic dome, patented by Fuller thirty years later.
Thus the first geodesic dome did not arise on the soil of the USA in the 1950s but rather in 1924, on the roof of the Zeiss factory in Jena, as a trial structure with a diameter of sixteen meters. Its construction, made of steel rods, was covered with wire mesh and shotcreted by the Munich company Dyckerhoff & Widmann, with the thickness of the concrete shell amounting to only six centimeters. A total of 3840 steel rods with a rectangular cross-section of 22 x 8 mm and a length of 600 mm were manufactured by Zeiss with "optical" precision. The permitted length tolerance was only 1/20 mm, corresponding to 1/12,000 of the rod length.
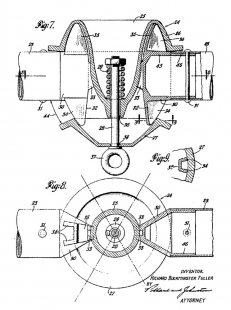
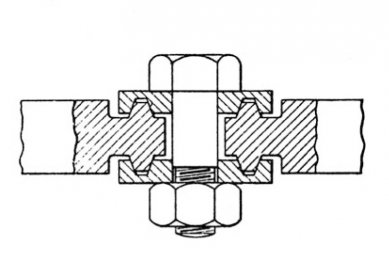
Identical geometry of Bauersfeld's and Fuller's constructions corresponds to the similarity of their joints. The function of Bauersfeld's joint is based on absolute "optical" manufacturing precision. It is made of two circular disks, in whose circular grooves the serrations made at the ends of the rods are clamped. Both disks are tightened with a single central screw, and the angular deviation from the tangential plane (i.e., the curvature of the sphere) is determined by the difference in radii of the two circular grooves.
Fuller’s joint saves weight and reveals an engineer skillful in aeronautical constructions. While it is more complicated, its elastic design allows for greater manufacturing and assembly tolerances. In this case, it is also a form of a clamp, but it consists of two hollow sheet metal castings that encompass the ends of the rods, which in the previous case were serrated but are now lens-shaped. The lenses are partially movable concerning the elastic design of the clamp in its cavity, automatically subjecting themselves to the curvature of the spherical surface. This clamp is also tightened by a central screw, to which a steel spring is added, ensuring flexibility in tightening.
It is more than unlikely that Fuller was unaware of Bauersfeld's construction. In the 1920s, it was frequently published by professional journals and protected by a patent in both the USA and many other countries. (14.1) The similarity of the two constructions can be explained as follows: After World War II, along with all German scientific material, the Zeiss company's archive was relocated to Wright Field Air Force Base in Dayton, Ohio, where it was subjected to expert analysis by American military professionals. It is not hard to imagine that Fuller, who had excellent ties with the military throughout his life, found here the opportunity for a detailed study of Bauersfeld's construction, although the name Bauersfeld (at least to the author's knowledge) does not appear in his work.
The sixteen-meter shell on the roof of the Jena factory was the first and last construction built by Zeiss based on five-fold symmetry. Subsequent constructions, known as "Zeiss-Dywidag," were already based on the triangulation of horizontal circumferences. This modification, while favorably impacting the simplification of production, allowing for a horizontal working joint instead of a five-fold symmetry, nevertheless signified a step back as far as the standardization of elements was concerned. While the first five-axis structure required only two lengths of rods, in the case of the second structure (the planetarium dome in Jena with a diameter of twenty-five meters), the number had to be increased to fifty-three. (15) This pragmatic, while geometrically not entirely clean yet technically functional construction was used by Zeiss throughout its existence. The last building of this kind was the planetarium in West Germany's Wolfsburg, built several years before the collapse of the GDR.
The SIAL nursery, a group of like-minded young graduates from the Czech Technical University in Prague, which was established with the author's participation in 1969 in northern Bohemia's Liberec, was a product of the political vacuum that prevailed in then-Czechoslovakia during the time between the violent suppression of "socialism with a human face" and the gradual restoration of neo-Stalinism. Today, it is hard to imagine that precisely during this uncertain period, at a time of equally limited and unlimited possibilities, the SIAL nursery was working on its most technologically demanding project, the design of the upper station of the cable car to the 1,600-meter high Sněžka in the Krkonošše. This project aimed to replace the old building that had been destroyed by fire. Working conditions at the mountain summit were limited by extreme climatic conditions, and for transporting materials, only cable cars and helicopters were feasible. For this reason, it was clear that the construction would be divided into two technologically different phases. The first phase, the cable car station itself, was to be carried out using conventional cast concrete technology, while the second phase was proposed as a lightweight prefabricated construction transportable by air. The landing pad was to be part of the first phase and, after the completion of the construction, was to serve the mountain rescue service helicopter.
For the second phase of construction, a geodesic dome was logically chosen for several reasons. First, the sphere, i.e., the body connecting maximum volume with minimal surface, was the optimal form in terms of limiting thermal losses; second, it was advantageous both aerodynamically and statically. The three-quarter sphere, limited by a flat cut at the level of the lower pentagon of the base icosahedron, was divided into 15 spherical triangles, which also corresponded to the load-bearing structure inside the sphere. This structure consisted of seamless tubes with a diameter of 400 mm, supporting three floors with a pentagonal base, of which the first and last were to be movably connected to the shell structure. These floors were designed as steel grids, whose triangular fields were filled with shaped sheet metal and cast in concrete. This single "wet" operation was to be performed under the protection and in controlled climate of the outer shell. The work necessary for the execution of the second part of the construction was to fully utilize the infrastructure established by the first phase, including the cable car.
The spherical shell was divided into primary and secondary constructions. The primary construction of 240 mm diameter tubes corresponded to the basic five-axis subdivision of the icosahedron, while the secondary construction of 120/100 square tubes corresponded to the spherical division of the panel shell. Similarly to the Bauersfeld-Fuller construction, these elements were to be fastened by circular clamps. This relatively complicated design was significantly marked by the designer's uncertainty. A self-supporting shell seemed too risky considering the expected dynamic loads from the wind, and the shell material remained an unresolved question for a long time. Its resolution only came thanks to a certain company in Ejpovice near Plzeň, which manufactured polyurethane seats for buses and trams. These lightweight and self-supporting sandwich products precisely matched the criteria for the desired shell. The polyurethane integral panel subsequently developed for Sněžka by Ejpovice technicians consisted of an insulating polyurethane core compressed on both sides by a rigid load-bearing shell made of the same material. A certain number of panels were to be equipped with integrated unopenable glazing. Upon completion, the building was to include a restaurant, café, emergency accommodation cells, and a viewing terrace.
Both from the outside and the inside, the building was to exert an uncompromising technical impression, emphasizing the feeling of being in an extreme location. All subjective criteria were set aside; the objective technical parameters and their solutions at the highest possible level of contemporary technology became the only defined goal. Due to its technological demands, this project was the first of SIAL's works, completely freeing itself from the infantile forms of romantic "machinism," and in its objectivity of optimal technical solutions, it most closely approached the architecture of uncompromising technological determinism. To use the words of the radical promoter of "scientific functionalism" Hannes Meyer, it was a building that is "neither beautiful nor ugly, that wants to be evaluated only as a constructive invention." (16)
Despite the advanced state of project development, it was never realized. Even the printed posters with photomontages of the building on the peak of Sněžka were withdrawn because a publication ban was imposed on SIAL. Just like the nursery itself, this blow was a specific product of the uncertain times, whose possibilities were just as limited as unlimited. From this blow, SIAL never recovered. The growing despair led to a gradual erosion of the group, whose most drastic form was the emigration of its members. Such a path was eventually chosen by both leading designers of Sněžka, Dalibor Vokáč and Zdeněk Zavřel.
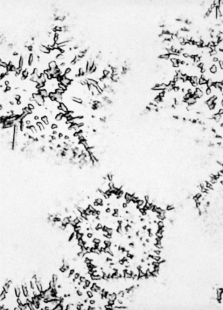
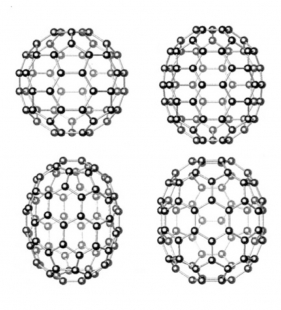
In 1982, a year before Fuller's death, several professional journals published a photograph that marked a scientific sensation. A ten thousand times enlarged image taken at the U.S. National Bureau of Standards laboratory depicted an aluminum and manganese alloy after its ultrafast cooling from liquid to solid state. The image clearly showed that matter can, under exceptional circumstances, organize itself in five-fold symmetry, i.e., in a form that had previously been considered excluded. Definitive confirmation of five-fold symmetry as an organizational scheme for matter came three years later, with the discovery of a new type of carbon molecule, whose sixty atoms are in a configuration identical to Bauersfeld-Fuller's geodesic dome construction. The authors of the discovery, Harold W. Kroto, Richard F. Smalley, and Robert F. Curl (Jr.), who received the Nobel Prize in Chemistry in 1996, named this new molecule "Buckminsterfullerene," often referred to in the scientific jargon as "Buckyball." (17) Today, carbon C60 is the subject of intense research since its extraordinary "energy-synergetic" rigidity is linked with justified hopes for its technical applications across various technological areas, from the production of highly resistant carbon fibers, through semiconductors and superconductors, to the production of artificial diamonds.
This story, which at first glance seems to be a mere episode from the field of physics and molecular chemistry, derives its uniqueness from the fact that the demonstrative model of carbon C60, discovered in 1985, was built as early as 1924 on the roof of the Zeiss factory in Jena, not to mention the vast number of subsequent constructions for civilian and military purposes. The discovery of carbon C60 provided satisfaction not only for Fuller’s "energy-synergetic" theory but also for the ancient theory concerning the analogous functions of the microcosm and macrocosm, leading us from contemporary molecular chemistry to the philosophical schools of ancient Greece.
The 17th-century French physicist, mathematician, and philosopher Blaise Pascal (1623-1662) is considered the author of the metaphor of the sphere as a volume of accumulated human knowledge, floating in the infinite space of the unknown. As the volume of knowledge increases, so too does the contact area with the unknown, so even the growing disproportion between the increase in knowledge cubed and the growth of the known unknown squared does not change the fact that the more we know, the more we know how little we know. Looking at the infinite space of the unknown, science seems to be a keyhole through which we occasionally get a glimpse into the Creator's workshop, whose dimensions are boundless. This realization of the infinity of human endeavor leads to both respect for the perfection of the Creator’s work and humility, which can be sensed from Richard Buckminster Fuller’s wise remark just before his death regarding his life’s work: "My task was not to preach God, but to serve God in silence about God."
Notes
1) The dangers of the descent lay in the unpredictable behavior of the steel cable oscillated by the ship's motion.
2) R. Mack, Modellstudien zum Tragverhalten der Kuppel des Pantheons. R. Graefe (ed.), Geschichte des Konstruierens, DVA Stuttgart 1989, pp. 38-43
3) D. Thode, Untersuchungen zur Lastabtragung in spätantiken Kuppelbauten. Studien zur Bauforschung Nr. 9., Koldewey-Gesellschaft, undated
4) O. Schubert, Gesetz der Baukunst, VEB E. A. Seemann Verlag Leipzig 1954, vol. II, p. 311
5) The equilateral triangle had, in Christian architecture, in addition to the symbol of the Holy Trinity, also a purely practical significance. In architectural practice, it allowed for an easy and fairly accurate transformation of the plans into reality (ad triangulum), and from the static perspective, the broken arch, constructed using a compass based on the equilateral triangle, graphically approximated what is otherwise difficult to construct—the catenary.
6) The analysis and criticism of the construction of St. Peter's Basilica's vault was primarily dealt with by Giovanni Poleni (1685-1761) in his work "Memorie istoriche delle Gran Cupolla del Tempio Vaticano" (1748). Known is also the more recent testimony from three learned monks (tre matematici), authored by Thommas Le Seur (1703-1770), Francesco Jaquier (1711-1788), and Ruggerio Giuseppe Boskovich (1711-1787), commissioned by Pope Benedict XIV and published in Rome in 1743.
7) In this context, the unfeasibility of Boullée's project for the National Library, whose vaulted ceiling was interrupted at its highest point by a long uncovered skylight, should be recalled.
8) E.-L. Boullée, Architektur - Abhandlung über die Kunst, Artemis-Verlag für Architektur, Zurich - Munich 1987, p. 75
9) The term "fruitful life" here does not lack a certain ironic touch, as one of Wallis’s numerous inventions was the so-called “spinning bomb,” a bomb that could skip considerable distances on water due to its rotation acting against the flight direction. The British RAF used this bomb to destroy German valley dams.
9.1) P. Jaray, whose patent was also used by the Kopřivnice company Tatra in the construction of its famous aerodynamic type 77, was also active for some time at the Prague University of Technology as an assistant in Professor Dörfl's department.
10) Deutsche Motor-Zeitschrift 5/6, 1924
11) K. Honzík, Tvorba životního slohu, Václav Petr, second edition, Prague 1947, Thoughts on Biotechnics, p. 234
12) See Thomas F. Banchoff, Dimensionen. Figuren und Körper in geometrischen Räumen, Spektrum Akademischer Verlag GmbH, Heidelberg 1991, p.102
13) The geodesic dome in Montreal complies only in its upper half with five-fold symmetry. Below the equatorial plane, the triangulation is applied to horizontal circumferences.
14) Archive of the Zeiss company in Jena. Author reviewed Bauersfeld's manuscript. This formulation of Bauersfeld is misleading. In reality, the same radii of circumscribed circles are not decisive, but rather the equal lengths of the sides of both polygons.
14.1) One of the many patents granted to Bauersfeld's construction was also the patent of the Czechoslovak Republic No. 14255 from November 10, 1924.
15) Das Zeiss Planetarium. Edited by Dr. Villiger, Head of the Astronomical Department of the Zeiss Factory, Jena, 7th undated edition, p. 51 and others.
16) C. Schnaidt, Hannes Meyer. Bauten Projekte und Schriften, Teufen 1965, p. 22
17) H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl, R. E. Smalley, C 60 - Buckminsterfullerene, Nature 318/1985, pp. 162-163
In 1934, a photograph of a skinny man, assisted by a reporter from NBC, emerged in the global press as he squeezed his long legs through a narrow 35-centimeter opening into the interior of a small iron sphere. This man was American zoologist William Beebe (1877-1962) and the cast-iron sphere, equipped with three small windows made of thick silica glass aside from the entry hole, was an instrument for exploring ocean depths. Beebe's friend, geologist and sphere designer Otis Barton, named his invention the "bathyscaphe." Within this 32-millimeter thick sphere, which had a diameter of just under 150 centimeters, both scientists undertook a series of descents, the most famous of which was the dizzying descent conducted in August 1934 in the Bermuda area, (1) which led to a depth of 923 meters previously unattained by anyone. This experiment coincided almost simultaneously with the ascent of Swiss researcher Professor Auguste Piccard (1884-1962) into the stratosphere. The aluminum gondola carried by a balloon with a maximum volume of 14,000 cubic meters was remarkably similar in shape and size to the bathyscaphe; however, due to the opposite direction of pressure effects, it required only a tenth of its thickness, amounting to just 3.5 millimeters in this case.
Unlike Beebe's "Russian roulette" descent, the danger of Piccard's ascent to a height of sixteen thousand meters was quite calculable, which in no way applied to the dangers associated with the inevitable return to earth. Auguste Piccard and his assistant Paul Kipfer likely did not devote too much attention to the landing issue - unlike Piccard's mother! She arrived at the site moments before takeoff and brought two wicker baskets, lined with soft cushions of her own making, to protect the precious heads of both researchers from undesirable damage. Just like Beebe's preparations before the Bermuda descent, the photograph of both serious scientists with quirky hats on their learned heads went down in the history of research as well as into the annals of subtle Swiss humor.
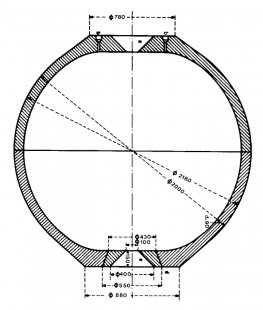
More than through his ascent into the stratosphere, "vertical professor" Piccard became famous for his oceanographic research, specifically the exploration of ocean depths using a submersible named "bathyscaphe." Just like the gondola of the airship, suspended from a body filled with hydrogen or helium, the gondola of the bathyscaphe is suspended from a float filled with gasoline. Just like an airship, the bathyscaphe also changes its position horizontally through motor power and vertically by taking in or releasing weight. The gondola of the bathyscaphe is also spherical, this time with a wall thickness of 90 mm. Unlike the bathyscaphe, molded from one piece, the gondola of the bathyscaphe is forged from two steel hemispheres. Since technically it is almost impossible to dimension the connection of both hemispheres to the pressures that vary with the depth reached (for example, by connecting with screws), the two hemispheres are glued together with Araldite after careful processing of the contact surfaces, the role of which, just like that of a relatively thin steel band in the connection area, is to prevent their mutual displacement. The perfect sealing of this ingeniously simple construction occurs automatically, in intensity corresponding to the depth reached.
This intelligent detail reminds us of a famous experiment carried out in 1663 by the learned mayor of Magdeburg Otto von Guericke (1602-1686), when he demonstrated that two freely placed spheres could withstand the force of a strong horse team when air was pumped out. This experiment was also associated with considerable personal risk. Matter was considered to be the expression of the Creator's will, as it was the only proof of His creative existence. From this perspective, a vacuum could therefore not exist, and the assertion of the opposite, i.e., the assertion of the existence of "nothing," was in the days when Aristotle's teaching on "horror vacui" was still an unshakable dogma of scholastic science, a life-threatening blasphemy.
From the described experiments, it is evident that a sphere is an ideal boundary between two different environments, whether as a protective shell of an "artificial living environment" or as a cover for "nothing." Scholastics, alongside Aristotle, believed in the finitude of the cosmos and its delimitation by a spherical surface as a perfect God-given form. The "heavenly dome" had already become an architectural metaphor for the builders of antiquity, and its architectural representation was both a cultural necessity and a significant technical problem calling for resolution.
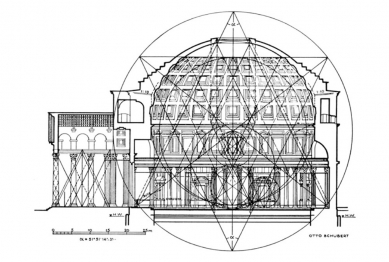
The dome of the Roman Pantheon, with a diameter of 43.2 m, is, when viewed from the inside, an exact hemisphere. It rests on a cylindrical drum, the height of which is equal to its radius, so it is possible to inscribe a sphere into the enclosed space, whose upper hemisphere completely fills the dome, while the imaginary lower hemisphere touches the floor at its exact geometric center with its "south pole." The fact that this magnificent structure has stood for nearly two millennia may be considered the most convincing evidence of its static capability; however, debates regarding the physical nature of this capability are still ongoing.
Today we know that the course of loading in a dome constructed of material capable of carrying only pressure acts along a curve corresponding to the shape of an inverted catenary. This curve must be demonstrated in approximately the inner third of the statically effective cross-section to prevent the proposed construction from collapsing. From shell theory, we know that the upper part of the spherical dome is stressed by a centripetal horizontal component of forces, while its lower part is stressed by a horizontal centrifugal component. The reversal of both forces occurs at the intersection point of the upper hemisphere with a cone whose apex is located at the south pole of the lower hemisphere, and whose apex angle is approximately 51°. In a dome constructed of material capable of carrying only pressure, inevitable tearing of the structure occurs at the intersection point. To avoid this catastrophe for the Pantheon, it was necessary to adopt measures, of which this building offers several:
First, the sectional view reveals that the thickness of the masonry in the dome increases from top to bottom, from the opening (oculus) with a diameter of nine meters, which is somewhat its "lightest" part, down to the stepped external accumulation of mass in its lower part, whose role is to enhance the vertical component of forces through increased mass, thus bringing the resultant vector closer to the imagined catenary.
Second, the construction of the Pantheon is divided into several sectors, differing in the weight of the employed masonry. From bottom to top, the travertine of the foundational masonry alternates with a mixture of travertine and limestone in the lower section of the drum. The upper part of the drum and the lower part of the dome up to the level of the second ring of coffers are built of limestone; a mixture of limestone and brick serves as material at the third ring of coffers, and finally, a mixture of limestone and pumice is the masonry of the remaining upper portion of the dome.
Third, the interior side of the dome features twenty-eight coffers in five overlapping circles, whose dimensions—namely, width, height, and depth—increase downward due to the growing circle. In other words, while the ribs of the coffers limit the spherical surface, their bottoms limit the statically effective area, which, with the varying depth of the coffers, approaches that of a rotational paraboloid, i.e., the ideal shape of a pressure-loaded dome.
Proving this hypothesis was the objective of a research project undertaken by Reiner Graefe and Frei Otto at the Institute for Lightweight Structural Engineering at the University of Stuttgart. (2) The work began with a two-dimensional chain model, on which the catenary was represented as the resultant of the known weight of the masonry and the proposed annular forces. The unknown component of horizontal annular forces was simulated by chains of constant length (and hence constant weight), suspended above the point of their effect, so that the curvature could be inferred for the sought horizontal component. The acquired data were then entered into the final three-dimensional model to depict the course of forces in their overall influence. Here, the annular forces were represented by chain parallelograms, whose deformation corresponded to the magnitude of the horizontal force vectors in the corresponding section of the arch.
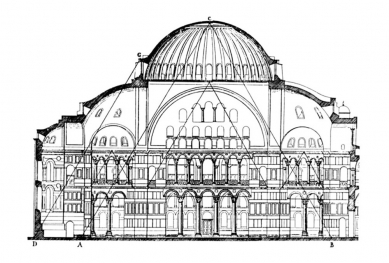
This experiment was, of course, merely a demonstration of a presumed situation and does not exclude further hypotheses. One of the other possibilities is elaborated by Dirk Thode in his dissertation (3) - he considers the upper part of the dome, i.e., the part that is centripetally stressed up to the point of force reversal, as a spherical shell and only proves the catenary below this plane. Perhaps the second hypothesis is somewhat closer to the truth; in any case, it receives intriguing support from the geometric analysis of the structure (4) performed by Otto Schubert. The triangulation of the Pantheon does not rest, as for example in the Hagia Sophia in Constantinople, on an equilateral triangle with an angle of 60° (5), but on an isosceles triangle with an apex angle of 51° 51' 14", i.e., with considerable accuracy concerning an angle known only to engineers of our time, and that from the aforementioned theory of shells. This affinity of form and its static arrangement is fascinating. It is a testament to the high technical level of a building that fully exhausts the scientific-technical possibilities of its time. Finally, only the exciting question remains of how much of what we now call shell theory was known to the builders of late antiquity in the early 2nd century AD.
After the construction of the Pantheon and the Hagia Sophia, attempts to realize a spherical dome nearly fell silent for an entire millennium. It was only in the 15th century that they revived with the constructions of the dome of the Florentine cathedral (42 m) and the dome of St. Peter's in the Vatican (40 m). However, these constructions deviate from our theme since they are double-skinned ribbed structures entirely consistent with the geometry of the catenary. In the case of the Florentine dome, spherical geometry was completely abandoned, and in the case of St. Peter's Basilica, its rendering in the soffit is merely an illusion. The scientific and technical significance of the dome of the Vatican temple lies primarily in the theoretical foundations of the statics of vaults, which were documented by savants of the 18th century in their research analyzing the structure and studying the damages that arose.
Entirely beyond the technical possibilities of spherical constructions constructed from material capable of transmitting only pressure (and thus only in projects) remained the spherical archetype of French revolutionary architecture at the end of the 18th century, of which the most famous and technically demanding example is "Newton's Cenotaph," authored by Etienne-Louis Boullée (1728-1799). Unfortunately, even a fleeting look at the construction of the gigantic sphere reveals its unfeasibility. (7) In section, we can recognize the eccentricity of the outer and inner boundaries of the sphere, favorably expressed in the varying thickness of the shell; however, this alone would not prevent the tearing of the structure at the point of reversal of the centripetal and centrifugal horizontal forces, already described in relation to the vault of the Pantheon. From a technical perspective, this gigantic building can at most be considered a visionary foretaste of reinforced concrete structures, which had yet to wait another 70 years. Although Françoise Ciognet (1814-1888) patented concrete as early as 1856, it took another 40 years for this unconventional material to be recognized by the famous École des Beaux-Arts, which only "stooped" to give lectures on concrete structures in 1897.
Boullée's project was both an architectural monument and a scientific instrument. Like the Pantheon, "Newton's Cenotaph" was an architectural representation of a heavenly dome, whose conical openings, symbolizing the starry sky, were directed toward the symbolic sarcophagus of the then greatest scientific authority, the famous English physicist Sir Isaac Newton. Boullée's project was created in 1784, five years before the outbreak of the French Revolution and—more importantly—a year after the ascent of the first balloon by the Montgolfier brothers. The gigantic dimensions and pathos of the work were expressions of a new era, whose horizon was exponentially widened due to the invention of aerostatic flight in both a transferred and a literal sense. The boundless space, i.e., a dimension that was previously only physical, became an imaginary aesthetic dimension. "The idea of greatness dominates our senses to such an extent that even the feeling of horror becomes a part of our admiration." (8) From these words, which Boullée used to comment on his project, resonates the notion of "beauty that terrifies" (horriblement belle), a concept promoted by the English thinker Edmund Burke (delightful horror) and German philosopher Immanuel Kant (die Schönheit des Schrecklichen), which became an integral part of European thinking by the end of the 18th century. In the aesthetic terminology of his time, this notion simultaneously describes "sublimity" (le sublime), which occupies one of the central roles in the architecture of the French Revolution. The temporal and thematic correlation of this new aesthetic dimension with the (relatively useless) invention of the Montgolfier brothers, as well as with the fascination of conquering the aerial sea in general, is evident.
The true expansion of this new aesthetic occurred in 1909 after Louis Blériot's sensational flight across the English Channel. Its most striking literary document is the aggressive staccato of the futurist manifesto published that same year by the Parisian newspaper "Le Figaro." This spirited and shockingly loud "foundation stone" of European modernism, authored by Italian poet Filippo Tommaso Marinetti, not only marked the beginning of a youthful, vital anti-bourgeois movement but was unfortunately also an artistic prelude to the industrial slaughter of both world wars, which plunged the European continent into a brutalism previously unknown and into the loss of cultural identity whose consequences we still feel.
Every reader of gruesome tales knows that horror can only be savored from the position of one's own safety, i.e., from the certainty that the domination of senses will not be followed by the domination of the physical body. In the case of more serious cultural subjects, such as fine arts and architecture, it is currently quite difficult for us to admit this aesthetic dimension, as its association with totalitarian ideologies is more than painful—whose repertoire extends beyond mere aesthetic horror to its physically perceptible realization. Perhaps it is precisely here that we must seek the reason why architecture of the "heroic style" (from Boullée to Speer) is generally rejected by even the most competent architectural critiques (from Sedelmayr to Posener). Nevertheless, this does not change the existence of forms of beauty that continue to tempt our "Faustian soul," regardless of whether we consider this feeling politically correct or not.
The morphological connection of the spherical archetype of the French Revolution with the invention of the aerostat is evident in terms of both a mere formal affinity with this new means of scientific and technological progress and in terms of the ideas of the Enlightenment about the global expansion of revolutionary ideas, the growth of sciences, and social reforms, concerning the political and scientific reconstruction of the world. In this form and with a similar significance, the spherical archetype also survives in the architecture of the Russian proletarian revolution, surprisingly at a time when aerostatic flight had long ceased to be a technically interesting alternative. In 1927, Ivan Ilyich Leonidov (1902-1959) used in his famous project "Institute V. I. Lenin" an aerostat quotation, in a form that in its monumental gesture matched the projects of the French Revolution. This project, which was a graduation work by a twenty-five-year-old student of the Moscow VCHUTEMAS school of art, captivated his contemporaries to such an extent that they prompted the young author to stay another two years at the school as an associate professor. Leonidov's project, which shines today with unparalleled modernity, is often cited as the pinnacle of Soviet constructivism. However, that does not change the fact that the answer to the pressing question of the technical execution of the glazed spherical auditorium, which, similar to "Newton's Cenotaph," was supposed to serve alternatively as a planetarium, remained (as is often the case with student works) a mystery to the author.
The so-called "geodesic construction," still regarded as the optimal technical mastery of spherical forms, is a term loosely related to aerostatic flight. The term was first used by Barnes N. Wallis (1887-1979), who, while working as a designer for Vickers, experimented with "geodesic" nets whose function was to stabilize and protect against damage the gas chambers inside the lifting bodies of English airships. Barnes N. Wallis, who remained true to the "geodesic" theme throughout his fruitful life (9), gained fame in 1933 for the unconventional design of the Vickers "Wellington" bomber, whose "geodesic" structure we would more accurately describe today as a laminate construction. Another expert in the field of aerostatic flight was Austrian aerodynamicist Paul Jaray (1889-1974), (9.1) who passionately debunked the still widely held naive assumption regarding a raindrop taking an aerodynamically clean "droplet" shape during its fall concerning the research of bodies of the least resistance. "Incomprehensible, if not downright miraculous, is the notion of a drop that tapers at the back and its uncritical circulation in literature. Nature has contributed nothing to this alleged 'insight.' (...) Many even believe they have seen the shape of a forward-expanding and backward-pointed drop with their own eyes; this can be explained by the fact that a drop hanging on a solid object adopts an elongated pear shape at the moment it attempts to leave this object due to gravity. This shape is derived from the interplay of gravity and surface tension. As soon as the drop detaches from this object, it takes on a spherical shape, which it then never abandons." (10)
The complementary effects of tension on the surface of a sphere and pressure within it are the cause of the stability of a series of natural forms, of which a classic and frequently cited example in literature is the stable system of cells on the spherical surface of an insect's eye. Karel Honzík, one of the architects of the Czech avant-garde and author of theoretical treatises, writes in his "Reflections on Biotechnics" about the balance between forces "centripetally collective" and "centrifugally individual." (11) This "state-forming" interpretation of a stable system as the result of complementary forces, expressed in the typically leftist jargon of the 1930s, is identical to the "energy-synergetic" theory developed by the multifaceted American engineer and philosopher Richard Buckminster Fuller (1895-1983). The "geodesic dome," for which Fuller is generally considered the inventor, is still recognized as both elegant and the ultimate mastery of the spherical form.
In the "energetic" part of his theory, Fuller separates local functions, while the "synergetic" part refers to natural organizing schemes that derive their stability from the synergetic interaction of complementary functions. In the case of the geodesic dome, it is the complementary properties of two Platonic bodies, the tetrahedron (a polyhedron with four equilateral triangles) as the fundamental scheme for the organization of matter in general and the icosahedron (a polyhedron with twenty equilateral triangles), which has properties that most closely resemble a sphere. Of all the regular polyhedra, the tetrahedron encloses the smallest volume with the greatest surface area, while the icosahedron, like a sphere, encloses the greatest volume with the least surface area. The tetrahedron and the icosahedron behave complementarily even under physical load. While the tetrahedron represents a form advantageous for loading with pressure, the icosahedron, like the sphere, represents a form advantageous for loading with tension. The connection of these complementary bodies occurs by joining the centroid (center) of the icosahedron with its twelve vertices, thus creating a concentric spatial truss of twenty tetrahedrons linked into a single icosahedron.
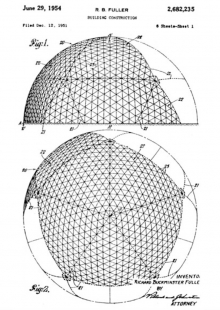
This seductive hypothesis, however, is unfortunately only an apparent possibility. The sides of the triangles on the surface of the icosahedron are actually about 5% longer than the sides directed towards its center. (12) This fact, which is referred to by solid-state physics as "frustration," leads to the conclusion that the compact assembly of spheres does not grow into an increasingly larger icosahedron, but forms what is known as a cuboctahedron, i.e., a polyhedron whose surface consists of eight equilateral triangles and six squares. By missing triangular connections at six points on this imagined spatial truss, this form is unstable. For this reason, the organizational scheme of matter based on the five-fold symmetry of the icosahedron was long excluded. This "attack" on "energy-synergetic" theory, however, did not stand in the way of the ingenious construction that Fuller patented in 1954 and successfully used in numerous military and civil constructions, including the USA Pavilion at Expo 67 in Montreal, Canada. (13)
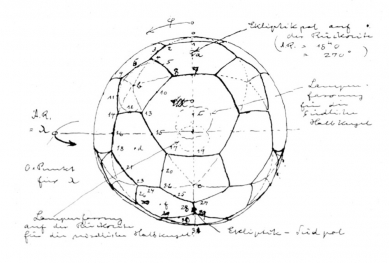
The problem of "frustration," however, is not the only shadow cast over the work of the American genius. In the early 1920s, the German Museum in Munich requested a project and the execution of a star projector from the Zeiss company in Jena, which was to become a part of the Munich planetarium. Walther Bauersfeld (1897-1959), who was commissioned with this work, developed not only the optical appliance but also the spherical shell construction, which was to serve as a projection surface. The resolution to this problem was described by Bauersfeld in his notes as follows: "If we imagine a regular body, the surface of which consists of twenty equilateral triangles, and we trim each of its twelve corners with a flat cut, we obtain a surface consisting of twenty hexagons and twelve pentagons. It is easy to choose the plane of the cut in such a way as to circumscribe both polygons with a circle of the same radius. The projection from the center of the resulting structure onto the surface of a sphere with the same center will then create an even distribution of the sphere." (14) Bauersfeld's prosaically and without "energy-synergetic" described process is nothing but a depiction of the geodesic dome, patented by Fuller thirty years later.
Thus the first geodesic dome did not arise on the soil of the USA in the 1950s but rather in 1924, on the roof of the Zeiss factory in Jena, as a trial structure with a diameter of sixteen meters. Its construction, made of steel rods, was covered with wire mesh and shotcreted by the Munich company Dyckerhoff & Widmann, with the thickness of the concrete shell amounting to only six centimeters. A total of 3840 steel rods with a rectangular cross-section of 22 x 8 mm and a length of 600 mm were manufactured by Zeiss with "optical" precision. The permitted length tolerance was only 1/20 mm, corresponding to 1/12,000 of the rod length.
Identical geometry of Bauersfeld's and Fuller's constructions corresponds to the similarity of their joints. The function of Bauersfeld's joint is based on absolute "optical" manufacturing precision. It is made of two circular disks, in whose circular grooves the serrations made at the ends of the rods are clamped. Both disks are tightened with a single central screw, and the angular deviation from the tangential plane (i.e., the curvature of the sphere) is determined by the difference in radii of the two circular grooves.
Fuller’s joint saves weight and reveals an engineer skillful in aeronautical constructions. While it is more complicated, its elastic design allows for greater manufacturing and assembly tolerances. In this case, it is also a form of a clamp, but it consists of two hollow sheet metal castings that encompass the ends of the rods, which in the previous case were serrated but are now lens-shaped. The lenses are partially movable concerning the elastic design of the clamp in its cavity, automatically subjecting themselves to the curvature of the spherical surface. This clamp is also tightened by a central screw, to which a steel spring is added, ensuring flexibility in tightening.
It is more than unlikely that Fuller was unaware of Bauersfeld's construction. In the 1920s, it was frequently published by professional journals and protected by a patent in both the USA and many other countries. (14.1) The similarity of the two constructions can be explained as follows: After World War II, along with all German scientific material, the Zeiss company's archive was relocated to Wright Field Air Force Base in Dayton, Ohio, where it was subjected to expert analysis by American military professionals. It is not hard to imagine that Fuller, who had excellent ties with the military throughout his life, found here the opportunity for a detailed study of Bauersfeld's construction, although the name Bauersfeld (at least to the author's knowledge) does not appear in his work.
The sixteen-meter shell on the roof of the Jena factory was the first and last construction built by Zeiss based on five-fold symmetry. Subsequent constructions, known as "Zeiss-Dywidag," were already based on the triangulation of horizontal circumferences. This modification, while favorably impacting the simplification of production, allowing for a horizontal working joint instead of a five-fold symmetry, nevertheless signified a step back as far as the standardization of elements was concerned. While the first five-axis structure required only two lengths of rods, in the case of the second structure (the planetarium dome in Jena with a diameter of twenty-five meters), the number had to be increased to fifty-three. (15) This pragmatic, while geometrically not entirely clean yet technically functional construction was used by Zeiss throughout its existence. The last building of this kind was the planetarium in West Germany's Wolfsburg, built several years before the collapse of the GDR.
The SIAL nursery, a group of like-minded young graduates from the Czech Technical University in Prague, which was established with the author's participation in 1969 in northern Bohemia's Liberec, was a product of the political vacuum that prevailed in then-Czechoslovakia during the time between the violent suppression of "socialism with a human face" and the gradual restoration of neo-Stalinism. Today, it is hard to imagine that precisely during this uncertain period, at a time of equally limited and unlimited possibilities, the SIAL nursery was working on its most technologically demanding project, the design of the upper station of the cable car to the 1,600-meter high Sněžka in the Krkonošše. This project aimed to replace the old building that had been destroyed by fire. Working conditions at the mountain summit were limited by extreme climatic conditions, and for transporting materials, only cable cars and helicopters were feasible. For this reason, it was clear that the construction would be divided into two technologically different phases. The first phase, the cable car station itself, was to be carried out using conventional cast concrete technology, while the second phase was proposed as a lightweight prefabricated construction transportable by air. The landing pad was to be part of the first phase and, after the completion of the construction, was to serve the mountain rescue service helicopter.
For the second phase of construction, a geodesic dome was logically chosen for several reasons. First, the sphere, i.e., the body connecting maximum volume with minimal surface, was the optimal form in terms of limiting thermal losses; second, it was advantageous both aerodynamically and statically. The three-quarter sphere, limited by a flat cut at the level of the lower pentagon of the base icosahedron, was divided into 15 spherical triangles, which also corresponded to the load-bearing structure inside the sphere. This structure consisted of seamless tubes with a diameter of 400 mm, supporting three floors with a pentagonal base, of which the first and last were to be movably connected to the shell structure. These floors were designed as steel grids, whose triangular fields were filled with shaped sheet metal and cast in concrete. This single "wet" operation was to be performed under the protection and in controlled climate of the outer shell. The work necessary for the execution of the second part of the construction was to fully utilize the infrastructure established by the first phase, including the cable car.
The spherical shell was divided into primary and secondary constructions. The primary construction of 240 mm diameter tubes corresponded to the basic five-axis subdivision of the icosahedron, while the secondary construction of 120/100 square tubes corresponded to the spherical division of the panel shell. Similarly to the Bauersfeld-Fuller construction, these elements were to be fastened by circular clamps. This relatively complicated design was significantly marked by the designer's uncertainty. A self-supporting shell seemed too risky considering the expected dynamic loads from the wind, and the shell material remained an unresolved question for a long time. Its resolution only came thanks to a certain company in Ejpovice near Plzeň, which manufactured polyurethane seats for buses and trams. These lightweight and self-supporting sandwich products precisely matched the criteria for the desired shell. The polyurethane integral panel subsequently developed for Sněžka by Ejpovice technicians consisted of an insulating polyurethane core compressed on both sides by a rigid load-bearing shell made of the same material. A certain number of panels were to be equipped with integrated unopenable glazing. Upon completion, the building was to include a restaurant, café, emergency accommodation cells, and a viewing terrace.
Both from the outside and the inside, the building was to exert an uncompromising technical impression, emphasizing the feeling of being in an extreme location. All subjective criteria were set aside; the objective technical parameters and their solutions at the highest possible level of contemporary technology became the only defined goal. Due to its technological demands, this project was the first of SIAL's works, completely freeing itself from the infantile forms of romantic "machinism," and in its objectivity of optimal technical solutions, it most closely approached the architecture of uncompromising technological determinism. To use the words of the radical promoter of "scientific functionalism" Hannes Meyer, it was a building that is "neither beautiful nor ugly, that wants to be evaluated only as a constructive invention." (16)
Despite the advanced state of project development, it was never realized. Even the printed posters with photomontages of the building on the peak of Sněžka were withdrawn because a publication ban was imposed on SIAL. Just like the nursery itself, this blow was a specific product of the uncertain times, whose possibilities were just as limited as unlimited. From this blow, SIAL never recovered. The growing despair led to a gradual erosion of the group, whose most drastic form was the emigration of its members. Such a path was eventually chosen by both leading designers of Sněžka, Dalibor Vokáč and Zdeněk Zavřel.
In 1982, a year before Fuller's death, several professional journals published a photograph that marked a scientific sensation. A ten thousand times enlarged image taken at the U.S. National Bureau of Standards laboratory depicted an aluminum and manganese alloy after its ultrafast cooling from liquid to solid state. The image clearly showed that matter can, under exceptional circumstances, organize itself in five-fold symmetry, i.e., in a form that had previously been considered excluded. Definitive confirmation of five-fold symmetry as an organizational scheme for matter came three years later, with the discovery of a new type of carbon molecule, whose sixty atoms are in a configuration identical to Bauersfeld-Fuller's geodesic dome construction. The authors of the discovery, Harold W. Kroto, Richard F. Smalley, and Robert F. Curl (Jr.), who received the Nobel Prize in Chemistry in 1996, named this new molecule "Buckminsterfullerene," often referred to in the scientific jargon as "Buckyball." (17) Today, carbon C60 is the subject of intense research since its extraordinary "energy-synergetic" rigidity is linked with justified hopes for its technical applications across various technological areas, from the production of highly resistant carbon fibers, through semiconductors and superconductors, to the production of artificial diamonds.
This story, which at first glance seems to be a mere episode from the field of physics and molecular chemistry, derives its uniqueness from the fact that the demonstrative model of carbon C60, discovered in 1985, was built as early as 1924 on the roof of the Zeiss factory in Jena, not to mention the vast number of subsequent constructions for civilian and military purposes. The discovery of carbon C60 provided satisfaction not only for Fuller’s "energy-synergetic" theory but also for the ancient theory concerning the analogous functions of the microcosm and macrocosm, leading us from contemporary molecular chemistry to the philosophical schools of ancient Greece.
The 17th-century French physicist, mathematician, and philosopher Blaise Pascal (1623-1662) is considered the author of the metaphor of the sphere as a volume of accumulated human knowledge, floating in the infinite space of the unknown. As the volume of knowledge increases, so too does the contact area with the unknown, so even the growing disproportion between the increase in knowledge cubed and the growth of the known unknown squared does not change the fact that the more we know, the more we know how little we know. Looking at the infinite space of the unknown, science seems to be a keyhole through which we occasionally get a glimpse into the Creator's workshop, whose dimensions are boundless. This realization of the infinity of human endeavor leads to both respect for the perfection of the Creator’s work and humility, which can be sensed from Richard Buckminster Fuller’s wise remark just before his death regarding his life’s work: "My task was not to preach God, but to serve God in silence about God."
Notes
1) The dangers of the descent lay in the unpredictable behavior of the steel cable oscillated by the ship's motion.
2) R. Mack, Modellstudien zum Tragverhalten der Kuppel des Pantheons. R. Graefe (ed.), Geschichte des Konstruierens, DVA Stuttgart 1989, pp. 38-43
3) D. Thode, Untersuchungen zur Lastabtragung in spätantiken Kuppelbauten. Studien zur Bauforschung Nr. 9., Koldewey-Gesellschaft, undated
4) O. Schubert, Gesetz der Baukunst, VEB E. A. Seemann Verlag Leipzig 1954, vol. II, p. 311
5) The equilateral triangle had, in Christian architecture, in addition to the symbol of the Holy Trinity, also a purely practical significance. In architectural practice, it allowed for an easy and fairly accurate transformation of the plans into reality (ad triangulum), and from the static perspective, the broken arch, constructed using a compass based on the equilateral triangle, graphically approximated what is otherwise difficult to construct—the catenary.
6) The analysis and criticism of the construction of St. Peter's Basilica's vault was primarily dealt with by Giovanni Poleni (1685-1761) in his work "Memorie istoriche delle Gran Cupolla del Tempio Vaticano" (1748). Known is also the more recent testimony from three learned monks (tre matematici), authored by Thommas Le Seur (1703-1770), Francesco Jaquier (1711-1788), and Ruggerio Giuseppe Boskovich (1711-1787), commissioned by Pope Benedict XIV and published in Rome in 1743.
7) In this context, the unfeasibility of Boullée's project for the National Library, whose vaulted ceiling was interrupted at its highest point by a long uncovered skylight, should be recalled.
8) E.-L. Boullée, Architektur - Abhandlung über die Kunst, Artemis-Verlag für Architektur, Zurich - Munich 1987, p. 75
9) The term "fruitful life" here does not lack a certain ironic touch, as one of Wallis’s numerous inventions was the so-called “spinning bomb,” a bomb that could skip considerable distances on water due to its rotation acting against the flight direction. The British RAF used this bomb to destroy German valley dams.
9.1) P. Jaray, whose patent was also used by the Kopřivnice company Tatra in the construction of its famous aerodynamic type 77, was also active for some time at the Prague University of Technology as an assistant in Professor Dörfl's department.
10) Deutsche Motor-Zeitschrift 5/6, 1924
11) K. Honzík, Tvorba životního slohu, Václav Petr, second edition, Prague 1947, Thoughts on Biotechnics, p. 234
12) See Thomas F. Banchoff, Dimensionen. Figuren und Körper in geometrischen Räumen, Spektrum Akademischer Verlag GmbH, Heidelberg 1991, p.102
13) The geodesic dome in Montreal complies only in its upper half with five-fold symmetry. Below the equatorial plane, the triangulation is applied to horizontal circumferences.
14) Archive of the Zeiss company in Jena. Author reviewed Bauersfeld's manuscript. This formulation of Bauersfeld is misleading. In reality, the same radii of circumscribed circles are not decisive, but rather the equal lengths of the sides of both polygons.
14.1) One of the many patents granted to Bauersfeld's construction was also the patent of the Czechoslovak Republic No. 14255 from November 10, 1924.
15) Das Zeiss Planetarium. Edited by Dr. Villiger, Head of the Astronomical Department of the Zeiss Factory, Jena, 7th undated edition, p. 51 and others.
16) C. Schnaidt, Hannes Meyer. Bauten Projekte und Schriften, Teufen 1965, p. 22
17) H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl, R. E. Smalley, C 60 - Buckminsterfullerene, Nature 318/1985, pp. 162-163
Mirko Baum: Streets at the End of the World – On Architecture and Other Matters, Kant 2007, pp. 48-69
The English translation is powered by AI tool. Switch to Czech to view the original text source.
















1 comment
add comment
Subject
Author
Date
také zajímavé
robert
19.03.10 01:22
show all comments
Related articles
0
19.04.2024 | Mirko Baum: From Machinism to Pelargoniums - Lecture at FUA TUL
0
12.03.2019 | Mirko Baum: Construction and Harmony
0
12.10.2017 | Mirko Baum: Part and Whole
0
01.12.2016 | Mirko Baum: Coincidence of Opposites
1
26.03.2010 | Mirko Baum: In the Magnetic Field of Gothic
0
15.03.2010 | Mirko Baum: About Bees and Screws





