Le Corbusier - MODULOR

The term "golden section" represents a proportional relationship based on the ratio of two parts of a whole. It is a proportion of parts A and B such that the smaller part A is to the larger part B exactly as the larger part B is to the whole A and B. The golden section is another proportional relationship that claims the status of a universal harmonic law in fields covering visual arts, music, architecture, as well as biology and plastic surgery.

Allegedly, this ratio was used by the ancient Egyptians almost five thousand years ago in the construction of the pyramids. The first written mentions of the golden section come from antiquity, from Hellenistic Greece by Euclid (circa 340-287 BC). In addition to Euclid, the ancient artist Phidias (sculptor, painter, goldsmith, and architect) also dealt with the golden section as early as the 5th century BC. He built the famous Athenian Parthenon on the Acropolis, whose foundation is a golden rectangle (see below), and the golden ratio can also be found in the façade of this building. According to some sources, the designation for the golden number (phi) was introduced in the 20th century after Phidias. Other sources state that this designation honors not Phidias, but Leonardo of Pisa, also known as Fibonacci (circa 1170-1240). The name of this significant mathematician is more related to the golden number from a mathematical perspective (see below). The theorist Vitruvius, the author of ten books on architecture, dealt with numerical dependencies and proportional relationships. He claimed that without this knowledge, it is impossible to build a beautiful building. According to Vitruvius, the aesthetics of a building are based on numerical relationships derived from the proportions of the human body. Today we know that the ratios of the sizes of parts of the human body often again approximate the golden number.

In modern architecture, the golden section was used by Le Corbusier (1887-1965). He dealt with geometry, through which he tried to understand the functioning of the universe and organic nature. Nature lives in harmony. Man as an individual emerged from nature; natural laws shape his life. We must first understand these laws and live in accordance with them; only then can we ensure a sense of harmony. He also argued that nature is the substance of mathematics, which at first glance appears to be a game of intertwined events. Therefore, for a person to ensure a suitable environment, he projected the system of nature into geometry. Through geometry, he sought the perfect proportion, which for him was represented by the golden section. With its help, he tried to invent a universal proportional unit that would be based on the human figure and would best express its purpose, that is, to serve humanity through utility.... it was the MODULOR.

"Mathematics is a magnificent structure created by man to provide him with an understanding of the universe"
LE CORBUSIER

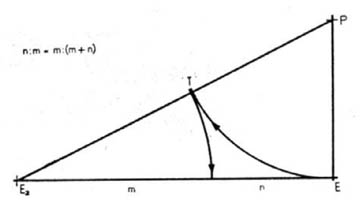NOTE: There are several geometric constructions of the golden section; the displayed variant is the most common

The golden section can also be expressed, apart from geometric means, as the ratio of one to the irrational number phi (pronounced "fee"), expressed using the formula (√5-1)/2), with a value of approximately 0.61803 (the so-called golden number). There is also a number Phi with a capital P at the beginning, which differs from phi by exactly one whole. Phi is thus approximately 1.61803 and is expressed by the formula (√5+1)/2). Phi is important primarily because it indicates the level to which the values of the so-called Fibonacci series gradually approach more and more.

There is another way to reach the golden number without using geometry — dividing a line segment. The golden number is closely related to the sequence of natural numbers (the so-called Fibonacci sequence), which was compiled by the Italian Leonardo of Pisa, also known as Fibonacci (who lived at the turn of the 12th and 13th centuries in Pisa). In 1202, he published his Latin work "Book of the Abacus" ("Incipit Liber Abbaci Compositus a Leonardo filius Bonacci Pisano"). In this book, he summarized all contemporary knowledge about arithmetic and algebra. It was one of the first books in Europe that taught how to use the decimal system. Until then, only Roman numerals were used. The Fibonacci sequence is a series of integers where the next member is always the sum of the two preceding members. The first member in the series is the number 1, the second is again 1, because before the number 1, we only find 0. The series then continues with the number 2 as the sum of 1+1. Therefore, the beginning of the series looks like this: 1,1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377... The ratio of each subsequent number in this series approaches the ratio of the golden section and thus also the number Phi. Namely, 1/1=1, 2/1=2, 3/2=1.5, 5/3=1.666..., 8/5=1.6, 13/8=1.625, 21/13=1.61538..., and it would be possible to continue with results getting ever closer to the number Phi.

The Fibonacci sequence is most often given using the so-called recurrent formula, this means that there is no formula for direct calculation of any member of the sequence, but a relation for calculating a member of the sequence using several preceding members. The general recurrent formula looks like this:

where pi are the members of the sequence, c1,.., ck (are constants and n, k are natural numbers. By this prescription, we have expressed the (n+k)-th member of the sequence using k preceding members. The number k is called the order of the recurrent formula.

The Fibonacci principle works in nature without our awareness of it. The author himself tested it when attempting to reproduce rabbits under ideal conditions. This example may seem detached from reality, but a further proof can be the reproduction of bees. Fibonacci numbers can also be found in the number of petals, for example: 3 (lily, iris), 5 (buttercup, carnation), 8 (daisy), 13 (buttercup). Even more fundamental is the structure of seed arrangements in flower heads (sunflower...), seeds of cones, cacti, the arrangement of leaves in some plants, or the shells of marine crustaceans (see image).

The Fibonacci sequence here proves to be a formula for optimal arrangement. The golden number can therefore indeed be introduced not only as a ratio of the lengths of two parts of a line segment but also as a limit of the aforementioned Fibonacci sequence.

Knowledge of the value of the golden number is not essential for everyday life. However, it is interesting how nature is governed by the ratio of the golden section. Searching for the golden section in plants, shells of mollusks, in the crystalline structures of materials, and even in the human body could fill a substantial book. This explains why this ratio has been so pleasing to people since the beginnings of civilization (and still is). Though most of us may not know about it, our eyes are accustomed to it. We perceive the golden section ratio as a natural thing. That is why it is still used today, for example, by architects, designers, painters, or photographers (sometimes even inadvertently) in their work.

Le Corbusier was literally enchanted by the golden section. This proportional system was used not only in the arrangement of facades of houses with horizontal windows but also in the interiors of buildings, for example, in the placement of artworks. During the Second World War, Le Corbusier moved from Paris to Vichy. For the first time in 1941, he began to create his own proportional canon, which he called modulor (mod/ modus - norm, or - gold). He wanted to create the ideal proportion of architecture, a space that would be in mutual harmony with man. His results were published in book form in 1948 in the first book Le Modulor (Paris) and in 1955 in the second expanded volume Le Modulor 2 (Paris).

The basis for the calculations and also for speculation represents the "typical" human body of an average European. The pattern of the human body is logical; the mutual relationship of man (the body) to architecture has historical roots back to antiquity and later to the Renaissance. Le Corbusier subjectively defined his anthropological model, claiming that as an architect-artist, he had the right to do so. How daring it is that he chose the male body of the average European height of 175 cm. He later adjusted this height to 183 cm, probably because dividing by the golden section yields "nicer" numbers. The sketch of the modulor does not represent the body of the "average" European but seemingly depicts an archaic figure of a Greek athlete: a slim waist, broad shoulders, and a small head on it. It denotes three distances on the human body that form the Fibonacci sequence of the golden section. Between the leg, the navel, the head, and the finger of the raised hand. Subsequently, he divides the height of the "average" European 175cm in the ratio of the golden section into scales of 108.2-66.8-41.45-25.4. (the value of 175 cm is more of the height of a typical Frenchman than a European). This last value represents exactly 10 inches, thus finding a connection with the English inch (which, however, does not apply to higher values). These numbers acquire human form, crucial points for spatial arrangement. They are therefore anthropological.

From this point, it can be admitted that this rule assigns main points to the space of the human form, expressing them in simpler, more substantial, mathematical development of values. The same applies to the unit, its double, and both extended or shortened golden sections. For the modulor to become an anthropological norm, it had to be universal for different length units. Therefore, Le Corbusier converted it from cm to feet or inches.

“Modulor is a scale tool based on the human form and mathematics."
LECORBUSIER

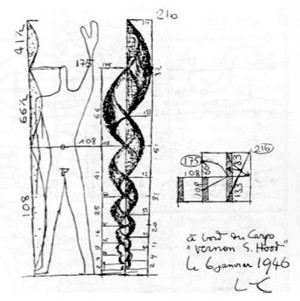The first graphical representation of the Modulor (1946) - height of a man 175cm

In 1946, Le Corbusier left for the USA, where he met at Princeton with Prof. Albert Einstein, who was also a member of the commission for the choice of the site of the UN building. He presented his discovery - the modulor. Einstein told Le Corbusier: “It's a system that makes the bad complex and the good simple”.

After obtaining a patent for the modulor, he presented his discovery to the public and published it in book form Le Modulor. He dares to claim that the modulor should be on every architect's drawing board, as it is an extraordinary aid in designing that removes all doubts and inaccuracies.

In 1947, Le Corbusier's height of the "average" person is conversely derived from 6 English feet, more precisely from 182.8 mm. By dividing according to the golden section, he obtains the so-called red series descending from above. When the steps of the red series are too large for practical needs, he creates another called the blue series, which arises from the value of 2260 mm (tip of the fingers of the raised hand), which is double the value of the red series. Through mathematical division using the golden section, fractions are rounded, resulting in differences of 7-10 mm above or below the so-called necessary values. When these basic values are converted to another length system - inches, another, independent system emerges from the original one.

Adjusted graphical representation of the Modulor (1947) - height of a man 182.8cm

The golden section rule has 3 values: 113, 70, 43cm (43+70=113 or 113-70=43). When adding: 113+70=183, 113+70+43=226. The three last values 113, 183, and 226 cm correspond to the designated space occupied by a person with a height of 180 cm. When applying the golden section rule to the value of 113 cm, it yields 70 cm. Thus, the first series, called the red one, is created: 4-6-10-16-27-43-70-113-183 etc... When using the golden section rule on the value of 226 cm (2x113), it yields 140-86cm. Thus, the second series, called the blue one, is created: 3-5-8-13-20-33-53-86-140-226-366-592 etc... Some values from the red and blue series have a remarkable relationship with human body values.

A table representing the space occupied by the human body in various positions

He presents his theoretical discoveries in 1951 at the Triennale in Milan, where a congress on proportions was simultaneously taking place with the participation of leading scientists, mathematicians, aestheticians, architects, and others. The Modulor does not remain only in the theoretical realm; Le Corbusier, based on it, designed an innovative building in the 1950s - a residential house, which with its interior arrangement and mixing of various functions had no precedent in architecture until then!

The theorist G.L. Hersley in his book titled Architecture and Geometry in the Age of Baroque dedicates space to Le Corbusier and his modulor. Geometry pervades LC's entire work, yet it never crystallized into a theory of architecture. The author states that the modulor has a close connection to the baroque geometry of R. Fludd, Kircher, and Kepler. LC distanced himself from the Renaissance and baroque and criticized his predecessors for the rational symmetry transferred into geometric plans, as he advocated for asymmetrical geometry. Yet, like them, he celebrated the effect of music, the human body as a source of measurement, the noble numbers, and their series and sequences. He was a pioneer of the ideal coordinate network where the cells of ideal quadrilaterals, used in the Renaissance and baroque, were located... This signals from where he derived even though he presented his theory externally and does not admit it himself.

When dividing the human body into three intervals (from foot to navel, from navel to top of the head, and from top of the head to the finger of the raised hand), he obtains three values: 108, 66½, and 41½. None of these lengths is actually part of the Fibonacci sequence and does not correspond to the ratio of the golden section! LC claims the exact opposite. The true Fibonacci series always starts with the number 1, while LC's series starts with the numbers 3 and 4, which is why he obtains different sequences.

(Proof: 108 : 66½ = 1.602; 66½ : 41½ = 1.624... the true value of the golden section is 1.618). In the first sketch of the modulor, alongside the "primitive" drawing of a man, two other scale series emerge that delineate areas. Perhaps they have a connection with the so-called sector, a baroque tool for measuring areas and volumes in different scales. Some values of the sequences are according to the Fibonacci series, some in the ratio of the golden section, and other are incorrect, outside these theories. LC assigns intervals on the human body, but the values 2, 9, and 11 can never fit the human body.

The ideal of the human figure (male) as a fundamental measure traces back to antiquity with Vitruvius. It is followed by Leonardo da Vinci with the drawing of a man inscribed in a circle and square (1485-1490). The baroque period brought with it an interest in numbers creating the human body. Robert Fludd (1574-1637) understood through it the essence of the entire cosmos. It is noteworthy that even LC's Renaissance and baroque predecessors did not have the correct proportions, just as the modulor does. The sketch of the modulor is imperfect. The figure has a very small square head without a face marked only by an outline, while the raised hand is bulky, lacking depicted fingers. LC's predecessors sought important proportional relationships even in details such as the human face, palm with fingers. LC did not attempt this at all; could it be that graphical representation is more important than reality or that he is camouflaging the imperfection of his figure?

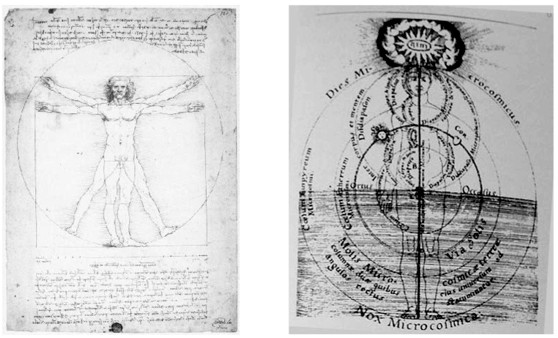Drawing of a man by L. da Vinci (1485-90) and drawing of a man by R. Fludd (1574-1637)

Nevertheless, LC's figure has an important relationship in common with L. da Vinci's figure. Both figures can be inscribed in both a circle and a square. The center of the circle is the navel, and the center of the square is the penis. In contrast, in Robert Fludd's figure, its center is the penis as the center of everything. Several of LC's collaborators, including Ellis Maillard, worked on the final version of the modulor. The original concept turns to R. Fludd. It adds circles of different sizes emanating from the centers of the squares of the basic sketch. The circles intersect each other just like in the baroque period with Fludd. There is no doubt about the conscious influence of the modulor by his microcosm.

In conclusion, G. L. Hersley states that the modulor was not constructed based on the golden section and Fibonacci series. If it had been, it would have been enough to simply change the values of the three-part division so that they would yield correctly. At the same time, it was not LC's aim to directly transfer it into architecture. The claim that the ratio 175:108 = 1.620 represents the value of the golden section 1.618 is incorrect. By adding squares and circles to the drawing of the modulor, purely linear squares arise that create modules. The modulor thus became the basis of the module... that was the result. By dividing squares in the golden ratio, further scale-variant squares, rectangles, and grids are created that, when transferred into construction, could represent the floor plans of houses, wall panels, doors, windows, and so we could continue into the individual details of the object.